Las combinaciones o coeficientes binomiales son una serie de números que indican la cantidad de formas en que se pueden extraer subconjuntos a partir de un conjunto dado.
En el poker nos sirven para realizar diferentes cálculos como el número de parejas que se pueden formar con las cartas del mismo rango de los cuatro palos de la baraja, o el número de flops posibles tanto en Texas Holdem como en Omaha.
Para calcular combinaciones hemos de utilizar la siguiente fórmula:
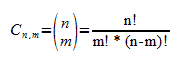
Para poder resolver un coeficiente binomial, hemos de saber calcular factoriales. Son muy sencillos. Su fórmula es n! = n*(n-1)* … *(n-n+1).
Te pongo un ejemplo: 4! = 4*3*2*1 = 24.
Podemos utilizar ambas fórmulas para calcular el número de parejas de ases que hay en la baraja.
Tenemos cuatro ases diferentes: el de tréboles (At), el de picas (Ap), el de corazones (Ac) y el de diamantes (Ad). Si los combinamos, teniendo en cuenta que no podemos repetir cartas y que nos da igual el orden en que nos las dé el croupier, podemos comprobar que hay seis parejas de ases diferentes:
- AtAp
- AtAc
- AtAd
- ApAc
- ApAd
- AcAd
Dicho número, 6, podríamos calcularlo utilizando la siguiente fórmula:
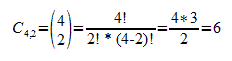
También podemos utilizar el número de flops posibles en Texas Holdem. Teniendo en cuenta que únicamente hemos visto nuestras dos cartas pre-flop, desconocemos otras 50, de las que el croupier descubrirá y colocará sobre la mesa 3. Por tanto, hemos de calcular las combinaciones de 50 cartas tomadas de tres en tres.
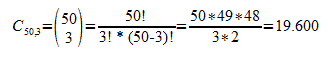
El número de flops posibles en Omaha es menor. Hemos visto cuatro cartas pre-flop, desconocemos 48 y el croupier o el dealer han de sacar 3 de la baraja para mostrarlas sobre la mesa. Por tanto, hemos de calcular las combinaciones de 48 cartas tomadas de tres en tres.
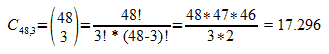

Hola,.
Muy buen desarrollo explicativo, y me acabas de ayudar mucho con mi tarea.
Espero encontrar mas contenido, con referencia mis tareas. Gracias.