En relación con el poker, podemos utilizar los porcentajes de probabilidad con objetivos muy diversos. No obstante, su uso fundamental tiene relación con dos conceptos fundamentales del juego:
- El dinero o los puntos que hemos de invertir en una mano, en el momento de tomar una decisión o hasta el final de la mano.
- Las opciones de victoria en la mano, bien en el momento de la toma de la decisión, bien en el showdown final.
En el transcurso de las manos, tanto en las sesiones de cash como en los torneos, es frecuente tener que calcular la probabilidad en porcentajes, especialmente cuando lainversión en el bote es grande (en relación con el tamaño de nuestra caja o stack), o incluso puede afectar a todo nuestro dinero o nuestros puntos (poniéndonos all-in) o a la caja completa del rival o los oponentes a los que nos estemos enfrentando.
Para poder relacionar ambos aspectos (inversión y probabilidad de victoria) hemos de tener cierta habilidad para realizar dos cálculos:
En primer lugar hemos de saber calcular la aportación al bote final que realizaremos nosotros, si hemos de pagar un all-in, o que realizará nuestro oponente, si es él quien ha de decidir entre igualar o no nuestro all-in.

Y en segundo lugar, deberemos realizar una conjetura más complicada y que dependerá, en gran medida, de nuestra lectura: la estimación de nuestra probabilidad devictoria respecto al rival. Si el all-in es pre-flop, la estimación dependerá de la suposición del rango de cartas del rival y de las opciones de victoria de nuestro par de cartas contra dicho conjunto. Si el all-in es post-flop, la estimación dependerá de la suposición de la jugada o el proyecto del rival.
Las dos situaciones más comunes durante el juego son las siguientes:
- Cuando nos atacan, hemos de estimar de la forma más ajustada posible las opciones de victoria de nuestras cartas al final de la mano y, a continuación, hemos de comparar dicho porcentaje con la proporción que supondría nuestra inversión en el bote total que quedaría si aceptamos pagar para ver las cartas restantes. Nuestro porcentaje estimado de probabilidad de victoria debe ser superior al porcentaje de nuestra aportación al bote total que quedará para poder aceptar el duelo.
- Cuando atacamos, hemos de estimar igualmente las opciones de victoria de nuestras cartas respecto a las que pueda tener nuestro rival y, a continuación,debemos apostar la cantidad necesaria para su porcentaje de probabilidad de victoria sea menor que el porcentaje de su inversión respecto al bote total que se llevará el ganador de la mano si el rival acepta el envite.
Vamos a ver un par de ejemplos de cálculo de aportación al bote final y de estimación de probabilidad de victoria.
En el primero, veremos una mano cuyas decisiones se toman en el pre-flop. Estamos en el big blind y el croupier nos ha dado AQo. El botón, que tiene un stack de 30 ciegas, realiza una subida pre-flop de 3 bb. El pequeño ciego se tira. Decidimos realizar una 3Bet a 9 ciegas y el oponente nos mete una 4B all-in, subiendo hasta 30 bb. A continuación, calculamos el porcentaje de aportación al bote final. Hemos de poner 21 bb en un bote que tendrá finalmente 60,5 bb. Por tanto, nuestro porcentaje de aportación al bote final será del 34,71%:
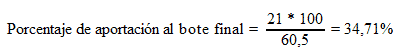
Para calcular el porcentaje estimado de victoria, necesitamos poner su 4B en un rango de cartas, es decir, debemos suponer con qué cartas nos lo puede estar haciendo. Para esta conjetura es muy útil tomar como referencia el dato de 4 Bet Range del jugador en el Holdem Manager. Imaginemos que su rango es de un 3,3%, es decir, está compuesto por los siguientes pares de cartas: AA, KK, QQ, JJ, AKso, AQs (JJ+, AQs+, AKo). Utilizando el Poker Stove podremos saber que nuestra probabilidad de victoria contra dicho conjunto es del 29,361%.
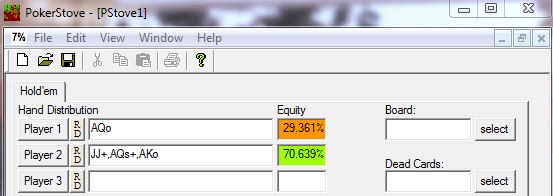
Por tanto, como nuestro porcentaje estimado de victoria es inferior a nuestra aportación al bote final, la decisión correcta es tirar las cartas.
Veamos ahora una situación con un all-in post-flop. Estamos en el cutoff, tenemos 100 ciegas de stack y el crouper nos ha dado ApJp. Nos llega la mano limpia (nadie ha subido previamente) y decidimos subir 4 ciegas. El pequeño ciego tira sus cartas y el grande, que tiene 25 ciegas, nos paga. Se monta un bote de 8,5 bb. El flop es Kc7p3p. Tenemos, por tanto, un proyecto de color (9 outs) y una overcard (3 outs); podemos sumarnos 12 outs. El big blind se pasa y metemos una apuesta de continuación de 6 bb. El ciego grande nos hace check-raise all-in a su resto, esto es, 21 bb. Hemos de pagar 15 bb para igualar el all-in. Por tanto, nuestra aportación al bote final será de un 29,70%:
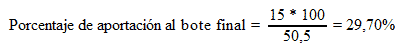
Si creemos que todos nuestros outs nos darán una jugada ganadora, podemos calcular que nuestra probabilidad de victoria, con 12 outs y 2 cartas comunes por venir, es de un 44,96%:
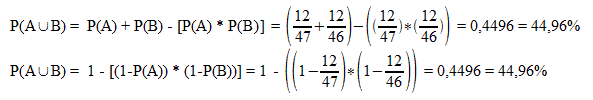
Por tanto, como nuestra probabilidad de victoria es considerablemente superior que nuestra aportación al bote final, podemos pagar el all-in del rival. Además, dado que el porcentaje de aportación solo es del 29,70%, no sobraría para pagar tener 7 outs (27,84% de victoria a dos cartas), número que tendríamos aun descontando cartas como Kp, que podrían ser peligrosas, dado que podrían dar full house al rival en el caso de que tuviese una trucha. Por consiguiente, se trata de un call a all-in bastante claro.
Si no tienes delante una tabla de outs, odds o resultados (o aún no la has memorizado), puedes recurrir a dos trucos para hacer los cálculos de estimación de victoria en función de outs. Se trata de dos sistemas bastante rudimentarios, pero que ofrecen resultados muy aproximados a los correctos:
- La “regla del 2″ sirve para calcular los porcentajes de victoria de la jugada con una carta (el turn o el river); consiste en multiplicar el número de outs por 2.
- La “regla del 4″ sirve para calcular los porcentajes de victoria de la jugada con dos cartas (el turn y el river); consiste en multiplicar el número de outs por 4.
