Es poco habitual ver cómo un croupier virtual o humano te da un full house en el flop. ¿Cuál es exactamente la probabilidad de que esto sucede?
Antes de hacer los cálculos, hemos de tener en cuenta que podemos conseguir un full servido en el flop, teniendo en mano una pareja o dos cartas distintas. Calculemos ambos casos utilizando la fórmula de la distribución multihipergeométrica.
Con pocket pair en mano (por ejemplo, 66):
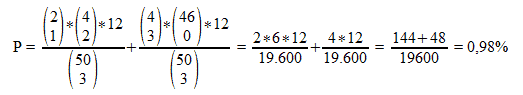
¿Cómo se puede interpretar la fórmula del full house con pareja en mano?
- P es la probabilidad de lograr dicha jugada en el flop.
- En el primer quebrado, contamos los full houses que consigues cuando consigues trío y aparecen dos cartas iguales en la mesa:
- 2 sobre 1 quiere decir que de los dos seises que puede haber en la baraja, debe salir uno en el flop.
- 4 sobre 2 quiere decir que de las cuatro cartas de un determinado rango, dos deben salir en el flop.
- Hemos de multiplicar por 12, ya que existen 12 posibilidades de que salga una pareja en el flop (13-1, descontando el rango 6).
- 50 sobre 3 quiere decir que el flop lo compondrán 3 cartas de las 50 que desconocemos.
- En el segundo quebrado, contamos el resto de full houses, esto es, los que se forman cuando salen tres cartas iguales en el flop (evidentemente distintas de 6).
- 4 sobre 3 quiere decir que de las cuatro cartas de un rango distinto de 6, salen tres cartas en el flop.
- 46 sobre 0 quiere decir que no sale ninguna carta de las restantes.
- Hemos de multiplicar por 12, ya que existen 12 posibilidades de que salgan tres cartas iguales en el flop (13-1, descontando el rango 6, ya que es imposible porque tenemos dos seises en mano).
Por tanto, la probabilidad de conseguir full house teniendo una pareja en mano es del 0,98%, lo que equivale a unas odds de 101,04 : 1.
También podemos conseguir full house en el flop teniendo dos cartas distintas en mano. En este caso, la fórmula sería la siguiente:
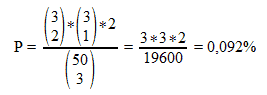
La fórmula se puede interpretar de la siguiente manera:
- P es la probabilidad de lograr dicha jugada en el flop.
- 3 sobre 2 quiere decir que de las tres cartas restantes de uno de nuestros rangos, salen dos cartas en el flop.
- 3 sobre 1 quiere decir que delrango de la otra carta que tenemos, sale una carta en el flop.
- Hemos de multiplicar por dos porque tenemos dos rangos distintos de cartas.
- 50 sobre 3 quiere decir que el flop lo compondrán 3 cartas de las 50 que desconocemos.
Por consiguiente, la probabilidad de conseguir un full house, teniendo en mano dos cartas distintas, es de un 0,092%, lo que se corresponde con unas odds de 1085,96 : 1.
